Домой Устройства Интегрирование методом замены переменной способ подстановки. Метод замены переменной (метод подстановки)

Устройства

Интегрирование методом замены переменной способ подстановки. Метод замены переменной (метод подстановки)

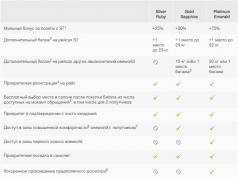
Тип занятия: изучение нового материала.

Учебно-воспитательные задачи:

научить учащихся применять метод интегрирования подстановкой;
продолжать формировать умения и навыки применения интегрирования функций;
продолжать формировать интерес к математике посредством решения задач;
воспитывать осознанное отношение к процессу обучения, прививать чувство ответственности за качество знаний, осуществлять самоконтроль за процессом решения и оформления упражнений;
напоминать, что только осознанное применение алгоритмов вычисления неопределенного интеграла позволит учащимся качественно усвоить изучаемую тему.

Обеспечение занятия:

таблица основных формул интегрирования;
карточки-задания для проверочной работы.

Студент должен знать: алгоритм вычисления неопределенного интеграла методом подстановки.

Студент должен уметь: применять полученные знания к вычислению неопределенных интегралов.

Мотивация познавательной деятельности студентов.

Преподаватель сообщает, что кроме метода непосредственного интегрирования существуют и другие методы вычисления неопределенных интегралов, одним из которых является метод подстановки. Это наиболее распространенный метод интегрирования сложной функции, состоящий в преобразовании интеграла с помощью перехода к другой переменной интегрирования.

Ход занятия

I . Организационный момент.

II . Проверка домашнего задания.

Фронтальный опрос:

III . Повторение опорных знаний учащихся.

1) Повторить таблицу основных формул интегрирования.

2) Повторить в чем заключается метод непосредственного интегрирования.

Непосредственным интегрированием называется такой способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.

IV . Изучение нового материала.

Вычислить заданный интеграл непосредственным интегрированием удается далеко не всегда, а иногда это связано с большими трудностями. В этих случаях применяют другие приемы. Одним из наиболее эффективных приемов является метод подстановки или замены переменной интегрирования. Сущность этого метода заключается в том, что путем введения новой переменной интегрирования удается свести заданный интеграл к новому интегралу, который сравнительно легко берется непосредственно. Если после замены переменной интеграл стал проще, то цель подстановки достигнута. В основе интегрирования методом подстановки лежит формула

Рассмотрим этот метод.

Алгоритм вычисления неопределенного интеграла методом подстановки:

Определяют, к какому табличному интегралу приводится данный интеграл (предварительно преобразовав подынтегральное выражение, если нужно).
Определяют, какую часть подынтегральной функции заменить новой переменной, и записывают эту замену.
Находят дифференциалы обеих частей записи и выражают дифференциал старой переменной (или выражение, содержащее этот дифференциал) через дифференциал новой переменной.
Производят замену под интегралом.
Находят полученный интеграл.
В результате производят обратную замену, т.е. переходят к старой переменной. Результат полезно проверять дифференцированием.

Рассмотрим примеры.

Примеры. Найти интегралы:

1) )4

Введем подстановку:

Дифференцируя это равенство, имеем:

V . Применение знаний при решении типовых примеров.

VI . Самостоятельное применение знаний, умений и навыков.

Вариант 1

Найти интегралы:

Вариант 2

Найти интегралы:

VII . Подведение итогов занятия.

VIII . Домашнее задание:

Г.Н. Яковлев, часть 1, §13.2, п.2, №13.13 (1,4,5), 13.15 (1,2,3)

На данном уроке мы познакомимся с одним из самых важных и наиболее распространенных приемов, который применяется в ходе решения неопределенных интегралов – методом замены переменной. Для успешного освоения материала требуются начальные знания и навыки интегрирования. Если есть ощущение пустого полного чайника в интегральном исчислении, то сначала следует ознакомиться с материалом , где я объяснил в доступной форме, что такое интеграл и подробно разобрал базовые примеры для начинающих.

Технически метод замены переменной в неопределенном интеграле реализуется двумя способами:

– Подведение функции под знак дифференциала ;
– Собственно замена переменной .

По сути дела, это одно и то же, но оформление решения выглядит по-разному.

Начнем с более простого случая.

Подведение функции под знак дифференциала

На уроке Неопределенный интеграл. Примеры решений мы научились раскрывать дифференциал, напоминаю пример, который я приводил:

То есть, раскрыть дифференциал – это формально почти то же самое, что найти производную.

Пример 1

Выполнить проверку.

Смотрим на таблицу интегралов и находим похожую формулу: . Но проблема заключается в том, что у нас под синусом не просто буковка «икс», а сложное выражение. Что делать?

Подводим функцию под знак дифференциала:

Раскрывая дифференциал, легко проверить, что:

Фактически и – это запись одного и того же.

Но, тем не менее, остался вопрос, а как мы пришли к мысли, что на первом шаге нужно записать наш интеграл именно так: ? Почему так, а не иначе?

Формула (и все другие табличные формулы) справедливы и применимы НЕ ТОЛЬКО для переменной , но и для любого сложного выражения ЛИШЬ БЫ АРГУМЕНТ ФУНКЦИИ ( – в нашем примере) И ВЫРАЖЕНИЕ ПОД ЗНАКОМ ДИФФЕРЕНЦИАЛА БЫЛИ ОДИНАКОВЫМИ .

Поэтому мысленное рассуждение при решении должно складываться примерно так: «Мне надо решить интеграл . Я посмотрел в таблицу и нашел похожую формулу . Но у меня сложный аргумент и формулой я сразу воспользоваться не могу. Однако если мне удастся получить и под знаком дифференциала, то всё будет нормально. Если я запишу , тогда . Но в исходном интеграле множителя-тройки нет, поэтому, чтобы подынтегральная функция не изменилась, мне надо ее домножить на ». В ходе примерно таких мысленных рассуждений и рождается запись:

Теперь можно пользоваться табличной формулой :

Готово

Единственное отличие, у нас не буква «икс», а сложное выражение .

Выполним проверку. Открываем таблицу производных и дифференцируем ответ:

Получена исходная подынтегральная функция, значит, интеграл найден правильно.

Обратите внимание, что в ходе проверки мы использовали правило дифференцирования сложной функции . По сути дела подведение функции под знак дифференциала и – это два взаимно обратных правила .

Пример 2

Анализируем подынтегральную функцию. Здесь у нас дробь, причем в знаменателе линейная функция (с «иксом» в первой степени). Смотрим в таблицу интегралов и находим наиболее похожую вещь: .

Подводим функцию под знак дифференциала:

Те, кому трудно сразу сообразить, на какую дробь нужно домножать, могут быстренько на черновике раскрыть дифференциал: . Ага, получается , значит, чтобы ничего не изменилось, мне надо домножить интеграл на .
Далее используем табличную формулу :

Проверка:

Получена исходная подынтегральная функция, значит, интеграл найден правильно.

Пример 3

Найти неопределенный интеграл. Выполнить проверку.

Пример 4

Найти неопределенный интеграл. Выполнить проверку.

Это пример для самостоятельного решения. Ответ в конце урока.

При определенном опыте решения интегралов, подобные примеры будут казаться лёгкими, и щелкаться как орехи:

В конце данного параграфа хотелось бы еще остановиться на «халявном» случае, когда в линейной функции переменная входит с единичным коэффициентом, например:

Строго говоря, решение должно выглядеть так:

Как видите, подведение функции под знак дифференциала прошло «безболезненно», без всяких домножений. Поэтому на практике таким длинным решением часто пренебрегают и сразу записывают, что . Но будьте готовы при необходимости объяснить преподавателю, как Вы решали! Поскольку интеграла в таблице вообще-то нет.

Метод замены переменной в неопределенном интеграле

Переходим к рассмотрению общего случая – метода замены переменных в неопределенном интеграле.

Пример 5

Найти неопределенный интеграл.

В качестве примера я взял интеграл, который мы рассматривали в самом начале урока. Как мы уже говорили, для решения интеграла нам приглянулась табличная формула , и всё дело хотелось бы свести к ней.

Идея метода замены состоит в том, чтобы сложное выражение (или некоторую функцию) заменить одной буквой .
В данном случае напрашивается:
Вторая по популярности буква для замены – это буква .
В принципе, можно использовать и другие буквы, но мы всё-таки будем придерживаться традиций.

Итак:
Но при замене у нас остаётся ! Наверное, многие догадались, что если осуществляется переход к новой переменной , то в новом интеграле всё должно быть выражено через букву , и дифференциалу там совсем не место.
Следует логичный вывод, что нужно превратить в некоторое выражение, которое зависит только от .

Действие следующее. После того, как мы подобрали замену, в данном примере, , нам нужно найти дифференциал . С дифференциалами, думаю, дружба уже у всех налажена.

Так как , то

После разборок с дифференциалом окончательный результат рекомендую переписать максимально коротко:
Теперь по правилам пропорции выражаем нужный нам :

В итоге:
Таким образом:

А это уже самый что ни на есть табличный интеграл (таблица интегралов , естественно, справедлива и для переменной ).

В заключении осталось провести обратную замену. Вспоминаем, что .

Готово.

Чистовое оформление рассмотренного примера должно выглядеть примерно так:

“

Проведем замену:

“

Значок не несет никакого математического смысла, он обозначает, что мы прервали решение для промежуточных объяснений.

При оформлении примера в тетради надстрочную пометку обратной замены лучше выполнять простым карандашом.

Внимание! В следующих примерах нахождение дифференциала расписываться подробно не будет.

А теперь самое время вспомнить первый способ решения:

В чем разница? Принципиальной разницы нет. Это фактически одно и то же. Но с точки зрения оформления задания метод подведения функции под знак дифференциала – гораздо короче .

Возникает вопрос. Если первый способ короче, то зачем тогда использовать метод замены? Дело в том, что для ряда интегралов не так-то просто «подогнать» функцию под знак дифференциала.

Пример 6

Найти неопределенный интеграл.

Проведем замену: (другую замену здесь трудно придумать)

Как видите, в результате замены исходный интеграл значительно упростился – свёлся к обычной степенной функции. Это и есть цель замены – упростить интеграл .

Ленивые продвинутые люди запросто решат данный интеграл методом подведения функции под знак дифференциала:

Другое дело, что такое решение очевидно далеко не для всех студентов. Кроме того, уже в этом примере использование метода подведения функции под знак дифференциала значительно повышает риск запутаться в решении .

Пример 7

Найти неопределенный интеграл. Выполнить проверку.

Пример 8

Найти неопределенный интеграл.

Замена:
Осталось выяснить, во что превратится

Хорошо, мы выразили, но что делать с оставшимся в числителе «иксом»?!
Время от времени в ходе решения интегралов встречается следующий трюк: мы выразим из той же замены !

Пример 9

Найти неопределенный интеграл.

Это пример для самостоятельного решения. Ответ в конце урока.

Пример 10

Найти неопределенный интеграл.

Наверняка некоторые обратили внимание, что в моей справочной таблице нет правила замены переменной. Сделано это сознательно. Правило внесло бы путаницу в объяснение и понимание, поскольку в вышерассмотренных примерах оно не фигурирует в явном виде.

Настало время рассказать об основной предпосылке использования метода замены переменной: в подынтегральном выражении должна находиться некоторая функция и её производная : (функции , могут быть и не в произведении)

В этой связи при нахождении интегралов довольно часто приходится заглядывать в таблицу производных.

В рассматриваемом примере замечаем, что степень числителя на единицу меньше степени знаменателя. В таблице производных находим формулу , которая как раз понижает степень на единицу. А, значит, если обозначить за знаменатель, то велики шансы, что числитель превратится во что-нибудь хорошее.

Замена многочлена или. Здесь - многочлена степени, например, выражение - многочлен степени.

Допустим, у нас есть пример:

Применим метод замены переменной. Как ты думаешь, что нужно принять за? Правильно, .

Уравнение приобретает вид:

Производим обратную замену переменных:

Решим первое уравнение:

Решим второе уравнение:

… Что это означает? Правильно! Что решений не существует.

Таким образом, мы получили два ответа - ; .

Понял как применять метод замены переменной при многочлене? Потренируйся сделать подобное самостоятельно:

Решил? Теперь проверим с тобой основные моменты.

За нужно взять.

Мы получаем выражение:

Решая квадратное уравнение, мы получаем, что имеет два корня: и.

Решением первого квадратного уравнения являются числа и

Решением второго квадратного уравнения - числа и.

Ответ : ; ; ;

Подведем итоги

Метод замены переменной имеет основных типа замен переменных в уравнениях и неравенствах:

1. Степенная замена, когда за мы принимаем какое-то неизвестное, возведенное в степень.

2. Замена многочлена, когда за мы принимаем целое выражение, содержащее неизвестное.

3. Дробно-рациональная замена, когда за мы принимаем какое-либо отношение, содержащее неизвестную переменную.

Важные советы при введении новой переменной:

1. Замену переменных нужно делать сразу, при первой же возможности.

2. Уравнение относительно новой переменно нужно решать до конца и лишь затем возвращаться к старому неизвестному.

3. При возврате к изначальному неизвестному (да и вообще на протяжении всего решения), не забывай проверять корни на ОДЗ.

Новая переменная вводится аналогичным образом, как в уравнениях, так и в неравенствах.

Разберем 3 задачи

Ответы на 3 задачи

1. Пусть, тогда выражение приобретает вид.

Так как, то может быть как положительным, так и отрицательным.

Ответ:

2. Пусть, тогда выражение приобретает вид.

решения нет, так как.

Ответ:

3. Группировкой получаем:

Пусть, тогда выражение приобретает вид
.

Ответ:

ЗАМЕНА ПЕРЕМЕННЫХ. СРЕДНИЙ УРОВЕНЬ.

Замена переменных - это введение нового неизвестного, относительно которого уравнение или неравенство имеет более простой вид.

Перечислю основные типы замен.

Степенная замена

Степенная замена.

Например, с помощью замены биквадратное уравнение приводится к квадратному: .

В неравенствах все аналогично.

Например, в неравенстве сделаем замену, и получим квадратное неравенство: .

Пример (реши самостоятельно):

Решение:

Это дробно-рациональное уравнение (повтори ), но решать его обычным методом (приведение к общему знаменателю) неудобно, так как мы получим уравнение степени, поэтому применяется замена переменных.

Все станет намного проще после замены: . Тогда:

Теперь делаем обратную замену:

Ответ: ; .

Замена многочлена

Замена многочлена или.

Здесь − многочлен степени, т.е. выражение вида

(например, выражение - многочлен степени, то есть).

Чаще всего используется замена квадратного трехчлена: или.

Пример:

Решите уравнение.

Решение:

И опять используется замена переменных.

Тогда уравнение примет вид:

Корни этого квадратного уравнения: и.

Имеем два случая. Сделаем обратную замену для каждого из них:

Значит, это уравнение корней не имеет.

Корни этого уравнения: и.

Ответ. .

Дробно-рациональная замена

Дробно-рациональная замена.

и − многочлены степеней и соответственно.

Например, при решении возвратных уравнений, то есть уравнений вида

обычно используется замена.

Сейчас покажу, как это работает.

Легко проверить, что не является корнем этого уравнения: ведь если подставить в уравнение, получим, что противоречит условию.

Разделим уравнение на:

Перегруппируем:

Теперь делаем замену: .

Прелесть ее в том, что при возведении в квадрат в удвоенном произведении слагаемых сокращается x:

Отсюда следует, что.

Вернемся к нашему уравнению:

Теперь достаточно решить квадратное уравнение и сделать обратную замену.

Пример:

Решите уравнение: .

Решение:

При равенство не выполняется, поэтому. Разделим уравнение на:

Уравнение примет вид:

Его корни:

Произведем обратную замену:

Решим полученные уравнения:

Ответ: ; .

Еще пример:

Решите неравенство.

Решение:

Непосредственной подстановкой убеждаемся, что не входит в решение этого неравенства. Разделим числитель и знаменатель каждой из дробей на:

Теперь очевидна замена переменной: .

Тогда неравенство примет вид:

Используем метод интервалов для нахождения y:

при всех, так как

Значит, неравенство равносильно следующему:

при всех, так как.

Значит, неравенство равносильно следующему: .

Итак, неравенство оказывается равносильно совокупности:

Ответ: .

Замена переменных - один из важнейших методов решения уравнений и неравенств.

Напоследок дам тебе пару важных советов :

ЗАМЕНА ПЕРЕМЕННЫХ. КРАТКОЕ ИЗЛОЖЕНИЕ И ОСНОВНЫЕ ФОРМУЛЫ.

Замена переменных - метод решения сложных уравнений и неравенств, который позволяет упростить исходное выражение и привести его к стандартному виду.

Виды замены переменной:

Степенная замена: за принимается какое-то неизвестное, возведенное в степень - .
Дробно-рациональная замена: за принимается какое-либо отношение, содержащее неизвестную переменную - , где и - многочлены степеней n и m, соответственно.
Замена многочлена: за принимается целое выражение, содержащее неизвестное - или, где - многочлен степени.

После решения упрощенного уравнения/неравенства, необходимо произвести обратную замену.

Замена переменной в неопределенном интеграле используется при нахождении интегралов, в которых одна из функций является производной другой функции. Пусть есть интеграл $ \int f(x) dx $, сделаем замену $ x=\phi(t) $. Отметим, что функция $ \phi(t) $ является дифференцируемой, поэтому можно найти $ dx = \phi"(t) dt $.

Теперь подставляем $ \begin{vmatrix} x = \phi(t) \\ dx = \phi"(t) dt \end{vmatrix} $ в интеграл и получаем, что:

$$ \int f(x) dx = \int f(\phi(t)) \cdot \phi"(t) dt $$

Эта и есть формула замены переменной в неопределенном интеграле .

Алгоритм метода замены переменной

Таким образом, если в задаче задан интеграл вида: $$ \int f(\phi(x)) \cdot \phi"(x) dx $$ Целесообразно выполнить замену переменной на новую: $$ t = \phi(x) $$ $$ dt = \phi"(t) dt $$

После этого интеграл будет представлен в виде, который легко взять основными методами интегрирования: $$ \int f(\phi(x)) \cdot \phi"(x) dx = \int f(t)dt $$

Не нужно забывать также вернуть замененную переменную назад к $ x $.

Примеры решений

Пример 1
Найти неопределенный интеграл методом замены переменной: $$ \int e^{3x} dx $$
Решение
Выполняем замену переменной в интеграле на $ t = 3x, dt = 3dx $: $$ \int e^{3x} dx = \int e^t \frac{dt}{3} = \frac{1}{3} \int e^t dt = $$ Интеграл экспоненты всё такой же по таблице интегрирования, хоть вместо $ x $ написано $ t $: $$ = \frac{1}{3} e^t + C = \frac{1}{3} e^{3x} + C $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Ответ
$$ \int e^{3x} dx = \frac{1}{3} e^{3x} + C $$

Метод основан на следующей формуле: ò f(x)dx = ò f(j(t)) j`(t) dt, где x = j(t) - функция, дифференцируемая на рассматриваемом промежутке.

Доказательство. Найдем производные по переменной t от левой и правой частей формулы.

Отметим, что в левой части находится сложная функция, промежуточным аргументом которой является x = j(t). Поэтому, чтобы дифференцировать ее по t, сначала дифференцируем интеграл по x, а затем возмем производную от промежуточного аргумента по t.

(ò f(x)dx)` t = (ò f(x)dx)` x *x` t = f(x) j`(t)

Производная от правой части:

(ò f(j(t)) j`(t) dt)` t = f(j(t)) j`(t) = f(x) j`(t)

Так как эти производные равны, по следствию из теоремы Лагранжа левая и правая части доказываемой формулы отличаются на некоторую постоянную. Поскольку сами неопределенные интегралы определены с точностью до неопределенного постоянного слагаемого, то указанную постоянную в окончательной записи можно опустить. Доказано.

Удачная замена переменной позволяет упростить исходный интеграл, а в простейших случаях свести его к табличному. В применении этого метода различают методы линейной и нелинейной подстановки.

а) Метод линейной подстановки рассмотрим на примере.

Пример 1. . Пусть t = 1 – 2x, тогда

dx = d(½ - ½ t) = - ½ dt

Следует отметить, что новую переменную можно не выписывать явно. В таких случаях говорят о преобразовании функции под знаком дифференциала или о введении постоянных и переменных под знак дифференциала, - т.е. о неявной замене переменной .

Пример 2. Например, найдем òcos(3x + 2)dx. По свойствам дифференциала
dx = (1/3)d(3x) = (1/3)d(3x + 2), тогда òcos(3x + 2)dx = ò(1/3)cos(3x + 2)d(3x +
+ 2) = (1/3)òcos(3x + 2)d(3x + 2) = (1/3)sin(3x + 2) + C.

В обоих рассмотренных примерах для нахождения интегралов была использована линейная подстановка t = kx + b (k ¹ 0).

В общем случае справедлива следующая теорема.

Теорема о линейной подстановке . Пусть F(х) - некоторая первообразная для функции f(х). Тогда òf(kx + b)dx = (1/k)F(kx + b) + C, где k и b - некоторые постоянные, k ¹ 0.

Доказательство.

По определению интеграла òf(kx + b)d(kx + b) = F(kx + b) + C. Ho
d(kx + b)= (kx + b)`dx = kdx. Вынесем постоянный множитель k за знак интеграла: kòf(kx + b)dx = F(kx + b) + C. Теперь можно разделить левую и правую части равенства на k и получить доказываемое утверждение с точностью до обозначения постоянного слагаемого.

Данная теорема утверждает, что если в определение интеграла ò f(x)dx = F(x) + C вместо аргумента х подставить выражение (kx + b), то это приведет к появлению дополнительного множителя 1/k перед первообразной.

С использованием доказанной теоремы решим следующие примеры.

Пример 3.

Найдем . Здесь kx + b = 3 – x, т.е. k = -1, b = 3. Тогда

Пример 4.

Найдем . Здесь kx + b = 4x + 3, т.е. k = 4, b = 3. Тогда

Пример 5.

Найдем . Здесь kx + b = -2x + 7, т.е. k = -2, b = 7. Тогда

Пример 6. Найдем . Здесь kx + b = 2x + 0, т.е. k = 2, b = 0.

Сравним полученный результат с примером 8, который был решен методом разложения. Решая эту же задачу другим методом, мы получили ответ . Сравним полученные результаты: . Таким образом, эти выражения отличаются друг от друга на постоянное слагаемое , т.е. полученные ответы не противоречат друг другу.

Пример 7. Найдем . Выделим в знаменателе полный квадрат.

В некоторых случаях замена переменной не сводит интеграл непосредственно к табличному, но может упростить решение, сделав возможным применение на последующем шаге метода разложения.

Пример 8. Например, найдем . Заменим t = x + 2, тогда dt = d(x + 2) = dx. Тогда

где С = С 1 – 6 (при подстановке вместо t выражения (x + 2) вместо первых двух слагаемых получим ½x 2 -2x – 6).

Пример 9. Найдем . Пусть t = 2x + 1, тогда dt = 2dx; dx = ½ dt; x = (t – 1)/2.

Подставим вместо t выражение (2x + 1), раскроем скобки и приведем подобные.

Отметим, что в процессе преобразований мы перешли к другому постоянному слагаемому, т.к. группу постоянных слагаемых в процессе преобразований можно было опустить.

б) Метод нелинейной подстановки рассмотрим на примере.

Пример 1. . Пусть t = - x 2 . Далее можно было бы выразить х через t, затем найти выражение для dx и реализовать замену переменной в искомом интеграле. Но в данном случае проще поступить по-другому. Найдем dt = d(-x 2) = -2xdx. Отметим, что выражение xdx является сомножителем подынтегрального выражения искомого интеграла. Выразим его из полученного равенства xdx = - ½ dt. Тогда

= ò (- ½)e t dt = (- ½)ò e t dt = (- ½)e t + C = (- ½) + C

Рассмотрим еще несколько примеров.

Пример 2. Найдем . Пусть t = 1 - x 2 . Тогда

Пример 3. Найдем . Пусть t = . Тогда

;